Burning Ship fractal

The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:

in the complex plane 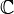which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann conditions.^[1]

1. ^ Michael Michelitsch and Otto E. Rössler (1992). "The "Burning Ship" and Its Quasi-Julia Sets". In: Computers & Graphics Vol. 16, No. 4, pp. 435–438, 1992. Reprinted in Clifford A. Pickover Ed. (1998). Chaos and Fractals: A Computer Graphical Journey — A 10 Year Compilation of Advanced Research. Amsterdam, Netherlands: Elsevier. ISBN 0-444-50002-2

Found Here: http://en.wikipedia.org/wiki/Burning_Ship_fractal

The images described here are generated by analysing the following series for each point (c_x,c_y) on the plane.

The grey level assigned to each point (cx,cy) is determined by how fast the series tends to infinity. For example, the points shown in black in the center of the form don't ever diverge to infinity. The points shown in light grey diverge very quickly. This is exactly the same technique used to create the Mandelbrot image. In all cases the starting point (x0,y0) is (0,0).

This fractal gets its name from the images obtained by zooming into regions along y=0 (x axis) an example is shown below

Source code

This C source code gives the basic idea of how the images on this page were created. As it stands it is run given a centre coordinate, a image width in world coordinates, and the name of the output file. It writes a raw RGB or greyscale image, this can be opened with most image editors or you can modify the code to save the image in your favorite format.

Found Here: http://local.wasp.uwa.edu.au/~pbourke/fractals/burnship/